[ DP ] 알고리즘 정리 및 문제
DP ( Dynamic Programming, 동적 계획법 )
하나의 큰 문제를 여러 개의 작은 문제로 나누어 계산하고 그 결과를 저장하여 문제를 해결할 때 똑같은 연산을 반복하지 않도록 하기위해 사용.
특정한 알고리즘이 아닌 하나의 문제해결 패러다임(방법론)
DP 사용 이유
이전에 방문/탐색/계산한 값을 저장하여 동일한 문제들을 반복하여 계산하게 되는 비효율적인 문제를 막을 수 있다.
ex ) 피보나치 수열문제에서 재귀로 함수를 구성하면, return f(n) = f(n-1) + f(n-2) 이며
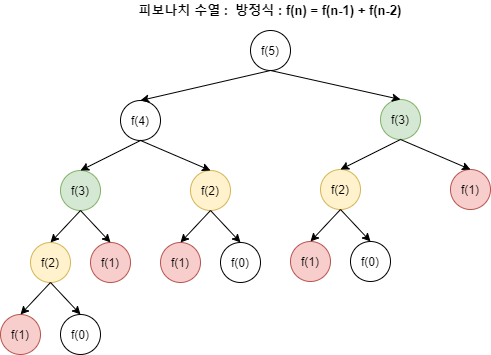
위의 사진과 같이 동일 부분을 반복 계산 하게된다. O(2^n)
하지만, DP 방식을 사용하면 앞에서 계산한 값을 다시 반복할 필요가 없기에,
O(n)으로 개선할 수 있다. ( 다항식 수준, 문제에 따라 다름 )
DP 사용 가능 조건 ( 2가지 )
a) 겹치는 부분 문제 ( Overlapping Subproblems )
동일한 작은 문제들이 반복해서 나타나며 + 같은 문제는 항상 정답이 같은 경우
&
b) 최적 부분 구조 ( Optimal Substructure )
부분 문제의 최적 결과 값을 사용해 전체 문제의 최적 결과를 나타낼 수 있는 경우
이 두 가지 조건이 충족한다면, 동적 계획법을 이용하여 문제를 풀 수 있다.
DP 가능여부 파악 및 사용
1) DP 가능여부 파악
2) 문제의 변수 파악
3) 변수 간 관계식 만들기 ( 점화식 )
4) 메모이제이션 (memoization(top-down) or tabulation(botton-up))
5) 기저 상태 파악하기
6) 구현하기
① DP 가능여부 파악
- 동일한 작은 문제들이 반복해서 나타나며 + 같은 문제는 항상 정답이 같은 경우
- 부분 문제의 최적 결과 값을 사용해 전체 문제의 최적 결과를 나타낼 수 있는 경우
위의 2가지를 만족하는지 파악
② 문제의 변수 파악
DP는 현재 변수에 따라 그 결과 값을 찾고 이용하여 재사용하는 것을 거친다. 즉, 문제 내 변수의 개수를 알아내야 한다. 이를 'state'를 결정한다고 한다.
예를 들어, 피보나치 수열에서는 n번째 숫자를 구하는 것이므로 n이 변수가 된다.
또한, 문자열 간의 차이를 구할 때는 문자열의 길이, Edit 거리 등 2가지 변수를 사용한다.
또, 유명한 Knapsack 문제에서는 index, 무게로 2가지의 변수를 사용한다. 이와 같이 해당 문제에서 어떤 변수가 있는지를 파악해야 그에 따른 답을 구할 수 있다.
문제 내 변수의 개수에 따라 DP 배열의 크기와 차원이 달라진다.
③ 변수 간 관계식 만들기 ( 점화식 만들기 )
변수들에 의해 결과 값이 달라지지만 동일한 변수값인 경우 결과는 동일하다. 그 결과값을 그대로 이용할 것이므로 이에 관한 관계식 (점화식)을 만들어낼 수 있어야 한다.
점화식의 반복/재귀를 통해 문제가 자동으로 해결되도록 구축할 수 있게 된다.
예를 들어 피보나치 수열에서는 f(n) = f(n-1) + f(n-2) 이다. 점화식은 변수의 개수, 문제의 상황마다 모두 다를 수 있다.
④ 메모이제이션
변수 간 관계식까지 정상적으로 생성되었다면 변수의 값에 따른 결과를 저장해야 한다. 이것을 메모한다고 하여 Memoization이라고 한다.
변수 값에 따른 결과를 저장할 배열 등을 미리 만들고 그 결과를 나올 때마다 배열 내에 저장하고 그 저장된 값을 재사용하는 방식으로 문제를 해결해 나간다. 보통 배열을 쓰며 변수의 개수에 따라 배열의 차원이 1~n차원 등 다양할 수 있다.
⑤ 기저 상태 파악 및 할당
여기까지 진행했으면, 가장 작은 문제의 상태를 알아야 한다. 보통 몇 가지 예시를 직접 손으로 테스트하여 구성하는 경우가 많다.
피보나치 수열을 예시로 들면, f(0) = 0, f(1) = 1과 같은 방식이다. 이후 두 가지 숫자를 더해가며 값을 구하지만 가장 작은 문제는 저 2개로 볼 수 있다.
해당 기저 문제에 대해 파악 후 미리 배열 등에 저장해두면 된다. 이 경우, 피보나치 수열은 매우 간단했지만 문제에 따라 좀 복잡할 수 있다.
⑥ 구현하기
개념과 DP를 사용하는 조건, DP 문제를 해결하는 과정도 익혔으니 실제로 어떻게 사용할 수 있는지를 알아보고자 한다. DP는 2가지 방식으로 구현할 수 있다.
a) Bottom-Up (Tabulation 방식) - 반복문 사용
이름에서 보이듯이, 아래에서부터 계산을 수행 하고 누적시켜서 전체 큰 문제를 해결하는 방식이다.
메모를 위해서 dp라는 배열을 만들었고 이것이 1차원이라 가정했을 때, dp[0]가 기저 상태이고 dp[n]을 목표 상태라고 하자. Bottom-up은 dp[0]부터 시작하여 반복문을 통해 점화식으로 결과를 내서 dp[n]까지 그 값을 전이시켜 재활용하는 방식이다.
Bottom-up일 때는 Memoization 이 아니라 Tabulation이라고 부른다.
왜냐면 반복을 통해 dp[0]부터 하나 하나씩 채우는 과정을 table-filling 이라고 하며, 이 Table에 저장된 값에 직접 접근하여 재활용하므로 Tabulation이라고 한다.
b) Top-Down (Memoization 방식) - 재귀 사용
dp[n]의 값을 찾기 위해 위에서부터 시작하여 dp[0]의 상태까지 내려간 다음, 해당 결과 값을 재귀를 통해 재활용하는 방식이다.
피보나치의 예처럼, f(n) = f(n-2) + f(n-1)의 과정에서 함수 호출 트리에서 보이듯, n=5일 때, f(3), f(2)에 대한 동일한 계산이 반복적으로 나오게 된다.
이 때, 이미 이전에 계산을 완료한 경우에는 계산하지 않고 단순히 메모리에 저장되어 있던 값을 꺼내어 활용하면 된다. 이렇듯 가장 최근의 상태 값을 메모해 두었다고 하여 Memoization 이라고 부른다.
Q. Divide and Conquer(분할 정복)와 차이점은?
분할 정복과 동적 프로그래밍은 주어진 문제를 작게 쪼개서 하위 문제로 해결하고 연계적으로 큰 문제를 해결한다는 점은 같다.
차이점은, 분할 정복은 분할된 하위 문제가 동일하게 중복이 일어나지 않는 경우에 쓰며, 동일한 중복이 일어나면 동적 프로그래밍을 쓴다는 것이다.
https://hongjw1938.tistory.com/47
문제 1. https://www.acmicpc.net/problem/11726
11726번: 2×n 타일링
2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오. 아래 그림은 2×5 크기의 직사각형을 채운 한 가지 방법의 예이다.
www.acmicpc.net
풀이코드 ( 접은 글 ⤵️)
연산 시마다 % 10,007을 해줘야하는 이유는
46번째부터 int 의 범위를 넘어가기 때문. (45번째가 1,836,311,903)
답을 구할 때 % 10,007을 해줘야하는데
오버플로우로 인한 값의 변화를 막기위해 미리미리 나머지 연산을 해줌
몫 quotient
나머지 remainder
나누는수 divisor
나누어지는수 dividend
나머지 연산의 분배법칙 [ a % c 를 a - q * d 로 바꿔서 증명가능 ]
(a+b)%c = ( a % c + b % c ) %c
(a*b)%c = ( a % c * b % c ) %c
(a-b)%c = ( a % c - b % c + c ) %c
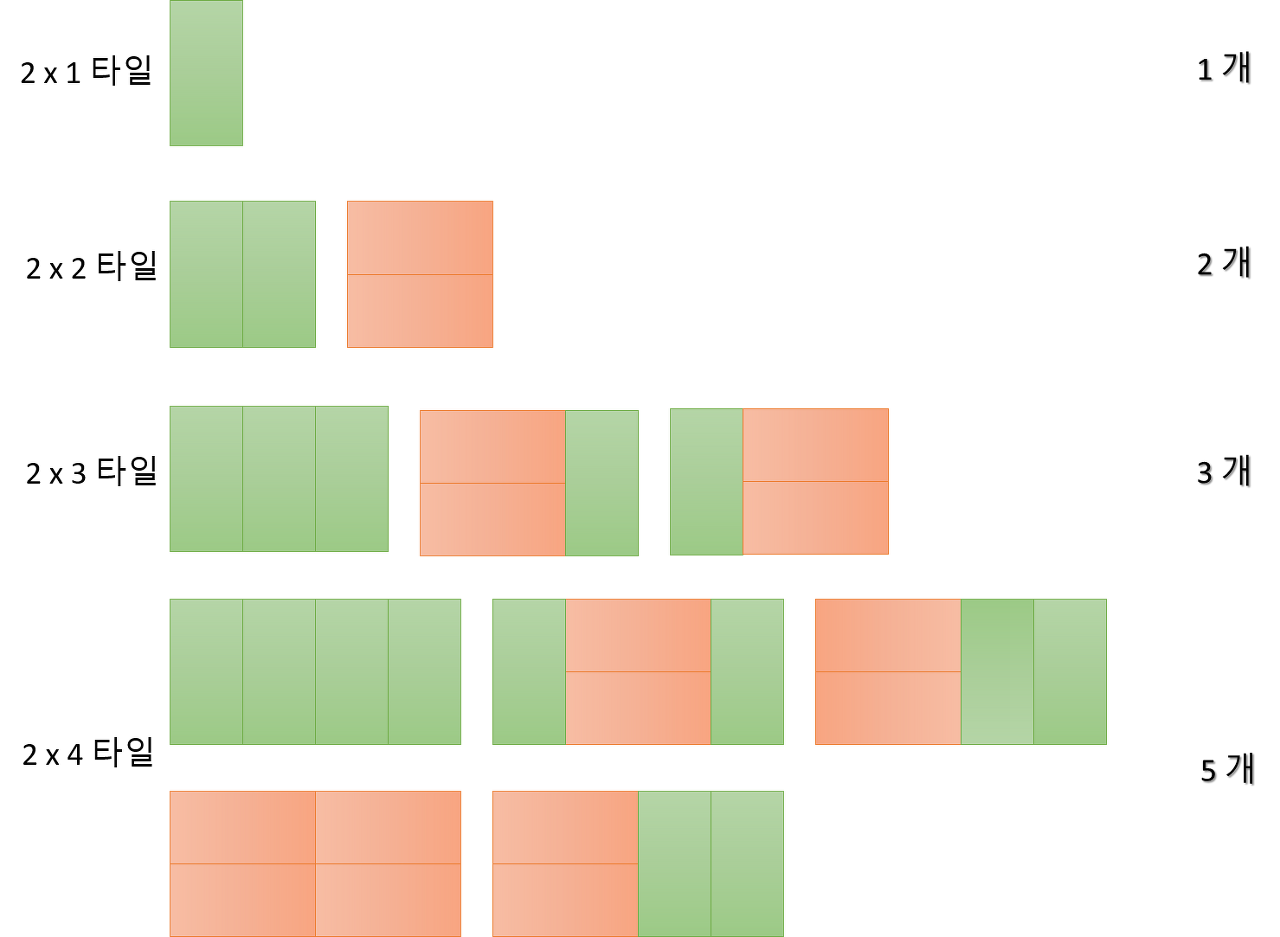
문제에서 2칸 단위로 분별을 해줘야함.
n번째는
n-1번째 에 만들어질 수 있는 모든 방법들(타일배치)에 2x1 타일을 추가로 붙여주거나
n-2번째에 만들어질 수 있는 모든 방법들(타일배치)에 1x2 타일을 추가로 붙여줘야함.
즉, DP[n] = DP[n-1] + DP[n-2]
#include <iostream>
#include <cstring>
using namespace std;
int DP[1001];
int n; // 2 x n 직사각형
void Sol()
{
for(int col = 3; col <= n; col++)
DP[col] = (DP[col - 1] + DP[col - 2])%10007;
}
int main()
{
DP[1] = 1;
DP[2] = 2;
cin >> n;
Sol();
cout << DP[n];
}문제 2 https://www.acmicpc.net/problem/2579
2579번: 계단 오르기
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점
www.acmicpc.net
https://www.acmicpc.net/problem/2618
2618번: 경찰차
첫째 줄에는 동서방향 도로의 개수를 나타내는 정수 N(5 ≤ N ≤ 1,000)이 주어진다. 둘째 줄에는 처리해야 하는 사건의 개수를 나타내는 정수 W(1 ≤ W ≤ 1,000)가 주어진다. 셋째 줄부터 (W+2)번째 줄
www.acmicpc.net
https://www.acmicpc.net/problem/5546
5546번: 파스타
상근이는 매일 저녁으로 파스타를 만들어 먹는다. 상근이가 만들 수 있는 파스타는 총 세 종류로 토마토 소스, 크림 소스, 바질 소스이다. 상근이는 앞으로 N일 동안 먹을 파스타를 계획하려고
www.acmicpc.net
풀이코드 ( 접은 글 ⤵️)
각각 크기는 인덱싱 편리성을 위해 +1씩 해주었으며, 날짜100+1, 파스타종류3+1, 연속일2+1로 설정해주었다.
그러므로 아래와 같이 선언을 해줄 수 있다.
int dp[101][4][3]; // i(0~100)일에 j(0~3)파스타를 먹었을 때 k(0~2)번 연속으로 먹는 경우의 수
------- ------- -------
변수를 파악하였으니, 점화식을 만들어야한다.
i번째 날일 때를 보면 dp[i][1..3][1..2] 총 6가지 경우가 나오며
차례대로 보면
dp[i][1][1] ( i번째날에 1번파스타를 1번연속으로 먹는 경우 )는 i-1번째인 전날에 2번파스타를 먹는 경우 + 3번파스타를 먹는 경우이다. // 전날에 1번 파스타를 먹는 경우엔 dp[i][1][2]에 더해줘야한다.
이 때, i-1번째날에 2번파스타를 먹는 경우를 보면 또 한번 나뉜다.
i-1번째날에 2번파스타를 1번연속 or 2번연속으로 나뉜다.
i-1번째날에 3번 파스타를 먹는 경우 또한 그렇다.
따라서,
dp[i][1][1] += ( dp[i-1][2][1] + dp[i-1][2][2] );
dp[i][1][1] += ( dp[i-1][3][1] + dp[i-1][3][2] ) 이다.
------- ------- -------
다음으로, dp[i][1][2]는 i-1번째날에 1번파스타를 1번연속으로 먹는 경우이다.
따라서,
dp[i][1][2] += dp[i-1][1][1];
------- ------- -------
이와 같은 방식으로, dp[i][2][1] 과 dp[i][2][2]. 그리고 dp[i][3][1]과 dp[i][3][2] 를 구하면
i번째 날의 경우의 수를 구할 수 있다.
-- 위의 방식은 bottom up 방식
* 피보나치 수열처럼 계속해서 더해지는 방식이기에 문제에서는 오버플로우를 막기위해 %10000 의 결과를 출력하라고 했다.
나머지연산의 분배법칙을 적용해야해서 매 연산마다 %10000을 해주었다.
//#define _CRT_SECURE_NO_WARNINGS
#include <bits/stdc++.h>
#include <unordered_map>
using namespace std;
// https://www.acmicpc.net/problem/5546
int dp[101][4][3]; // i(0~100)일에 j(0~3)파스타를 먹었을 때 k(0~2)번 연속으로 먹는 경우의 수
int main()
{
//freopen("input.txt", "r", stdin);
int n, k;
cin >> n >> k;
unordered_map<int, int> day_pasta;
int day, pasta;
for (int i = 0; i < k; i++)
{
cin >> day >> pasta;
day_pasta[day] = pasta;
}
// 첫날
if (day_pasta.find(1) != day_pasta.end()) // 파스타 정해진 날
dp[1][day_pasta[1]][1] = 1;
else
{
dp[1][1][1] = 1;
dp[1][2][1] = 1;
dp[1][3][1] = 1;
}
for (int i = 2; i <= n; i++)
{
if (day_pasta.find(i) != day_pasta.end()) // i번째 날은 파스타 day_pasta[i]로 정해진 날
{
for (int j = 1; j <= 3; j++)
{
if(j != day_pasta[i])
dp[i][day_pasta[i]][1] += (dp[i - 1][j][1] + dp[i - 1][j][2]) % 10000;
}
dp[i][day_pasta[i]][2] += dp[i - 1][day_pasta[i]][1] % 10000;
}
else
{
for (int j = 1; j <= 3; j++)
{
for (int jj = 1; jj <= 3; jj++)
{
if (j != jj)
dp[i][j][1] += ( dp[i - 1][jj][1] + dp[i - 1][jj][2] ) % 10000;
}
dp[i][j][2] += dp[i - 1][j][1] % 10000;
}
/*
dp[i][1][1] += ( dp[i - 1][2][1] + dp[i - 1][2][2] );
dp[i][1][1] += ( dp[i - 1][3][1] + dp[i - 1][3][2] );
dp[i][1][2] += dp[i - 1][1][1];
dp[i][2][1] += (dp[i - 1][1][1] + dp[i - 1][1][2] + dp[i - 1][3][1] + dp[i - 1][3][2]);
dp[i][2][2] += dp[i - 1][2][1];
dp[i][3][1] += (dp[i - 1][1][1] + dp[i - 1][1][2] + dp[i - 1][2][1] + dp[i - 1][2][2]);
dp[i][3][2] += dp[i - 1][3][1];
*/
}
}
int result = 0;
for (int j = 1; j <= 3; j++)
{
for (int k = 1; k <= 2; k++)
{
result += dp[n][j][k] % 10000;
}
}
cout << result % 10000;
}https://www.acmicpc.net/problem/23256
23256번: 성인 게임
각 테스트 케이스마다 만들 수 있는 서로 다른 칼날의 개수를 $1\,000\,000\,007$로 나눈 나머지를 출력하라.
www.acmicpc.net
풀이코드 ( 접은 글 ⤵️)
i-1번째에서 i번째 칼날로 넘어갈 때, 2가지의 경우로 나뉜다.
a) i-1번째 칼날의 오른쪽에 3칸의 광석을 추가하는 경우
b) i-1번째 칼날의 맨오른쪽 하나의 광석을 뺀 모습에 2x1 광석을 추가하는 경우
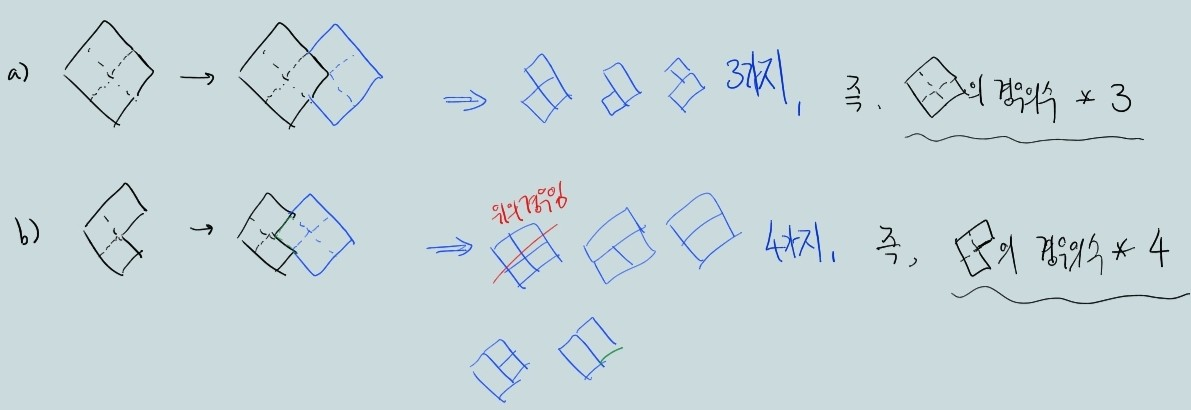
이 때, 맨 오른쪽 광석이 한칸씩 빠진 < 모양의 경우의 수도 관리를 해줘야하기에 2개의 dp 배열을 사용했다.
오른쪽 끝 블록이 차있으면 Full_DP으로, 안차있는 < 모양이면 NotFull_DP로 관리해주었다.
이에 따른 Full_DP[i] 의 점화식은
Full_DP[i] = Full_DP[i-1]*3 + NotFull_DP[i-1]*4;
NotFull_DP[i-1] 의 점화식을 모르기에, NotFull_DP[i]의 점화식에 대해 얘기하자면
이전의 NotFull_DP[i-1] 모양에 2x1 광석 하나와 1x1 광석 하나를 붙이는 경우 2가지
+ 1x1 광식 세개를 붙이는 경우 1가지가 있다.
따라서, NotFull_DP[i] 의 점화식은
NotFull_DP[i] = Full_DP[i-1] + NotFull_DP[i-1]*2;
N 의 최대값이 1,000,000이므로 구하는 과정에서 오버플로우하기에, %1,000,000,007을 해주라고 한다.
나머지의 값은 10억 6 이하인데, 2번까지는 괜찮다쳐도 3번 이상 더할 시, int형의 범위를 벗어나 오버플로우가 발생할 가능성이 있다.
이를 막기위해 바로 *3 *4를 해주는 식이 아니라,
1번씩 더해주면서 그 때마다 % 1,000,000,007을 해주었다.
#define _CRT_SECURE_NO_WARNINGS
#include <bits/stdc++.h>
using namespace std;
// https://www.acmicpc.net/problem/23256
int Full_DP[1000001];
int NotFull_DP[1000001];
const int divisor = 1000000007;
int Calc(int num, int m)
{
int result = 0;
for (int i = 0; i < m; i++)
{
result = (result + num) % divisor;
}
return result;
}
int main()
{
freopen("input.txt", "r", stdin);
int t,n;
cin >> t;
vector<int> nums;
for (int i=0; i < t; i++)
{
cin >> n;
nums.push_back(n);
}
int maxN = *max_element(nums.begin(), nums.end());
Full_DP[1] = 7;
NotFull_DP[1] = 3;
for (int i = 2; i <= maxN; i++)
{
// (Full_DP[i - 1] % divisor * 3 + NotFull_DP[i - 1] * 4) % divisor;
Full_DP[i] = (Calc(Full_DP[i - 1], 3) + Calc(NotFull_DP[i - 1], 4)) % divisor;
// NotFull_DP[i] = (Full_DP[i - 1] + NotFull_DP[i - 1] * 2) % divisor;
NotFull_DP[i] = (Full_DP[i - 1] + Calc(NotFull_DP[i - 1], 2)) % divisor;
}
for (int n : nums)
cout << Full_DP[n] % divisor << '\n';
return 0;
}https://www.acmicpc.net/problem/12762
12762번: 롤러코스터
첫째 줄에 개조하고자 하는 구간의 길이 \(N\)이 주어진다. 구간의 길이는 1,000을 넘지 않는 자연수이다. 둘째 줄에 구간 내에 있는 각 기둥들의 높이가 주어진다. 기둥의 높이는 10,000 이하의 자연
www.acmicpc.net
기둥 높이들은 vector<int> pillar로 선언해주었다.
롤러코스터의 진행방향은 공사가 끝난 후에 정해진다. 그렇기에 하이라이트 구간은
⬉⬈ or ⬉ or ⬈ 모양이 될 수 있다.
하이라이트 구간의 가장 낮은 지점(높이의 기둥)을 중심기둥이라고 칭해보자
가장 하이라이트 길이가 긴 구간의 중심(기둥)을 알아야하고 이 때의 하이라이트 구간 길이를 출력해야한다.
이를 위해서는 중심을 1번 기둥부터 n번 기둥까지로 정해가면서 왼쪽위와 오른쪽위로 올라가는 것으로 볼 수 있다.
즉, (중심으로부터 1번기둥까지의 최대 오르막 길이 ) + ( 중심기둥부터 마지막기둥(n번)까지의 최대 오르막 길이 ) 들 중에서 최대값을 찾아야한다.
주어진 테스트케이스로 생각해보자.
처음에는 (1 ← 1) + (1 → 5)
두번째는 (1 ← 2) + (2 → 5)
세번째는 (1 ← 3) + (3 → 5)
네번째는 (1 ← 4) + (4 → 5)
마지막은 (1 ← 5) + (5 → 5) 이다.
그렇기에 1 ← 중심 들을 관리하는 배열인 int LeftUp[1001] 배열과
그렇기에 중심 → n 들을 관리하는 배열인 int LeftUp[1001] 배열을 사용해주었다.
예를들어,
LeftUp[4]은 3 ~ 1번 기둥들을 중심기둥으로 했을 때의 값들을 보면서 구해준다. 중심기둥 값인 pillar[4] 와 pillar[3]~pillar[1]를 비교하여 4번 기둥이 3~1번 기둥보다 더 낮을 때,
왼쪽위로의 구간의 최대값을 찾아주면 된다.
반대로, RightUp[2] 는 3~5번 기둥들을 따져주면 된다.
그러므로, DP로 구해줄 수 있다.
LeftUp배열과 RightUp배열을 다 구해준 후에, 위에서 봤던
처음에는 (1 ← 1) + (1 → 5)
두번째는 (1 ← 2) + (2 → 5)
세번째는 (1 ← 3) + (3 → 5)
네번째는 (1 ← 4) + (4 → 5)
마지막은 (1 ← 5) + (5 → 5) 이 작업을 해주면 된다.
LeftUp[x]+RightUp[x] 값 중 최대값을 찾아주면된다.
이 때, 중심기둥이 겹치므로 마지막에 -1을 해주었다.
#define _CRT_SECURE_NO_WARNINGS
#include <bits/stdc++.h>
using namespace std;
// https://www.acmicpc.net/problem/12762
int LeftUp[1001];
int RightUp[1001];
int main()
{
freopen("input.txt", "r", stdin);
int n, h;
vector<int> pillar; // 기둥 높이
pillar.push_back(0);
cin >> n;
for(int i=0; i<n; i++)
{
cin >> h;
pillar.push_back(h);
}
LeftUp[1] = 1;
RightUp[n] = 1;
// LeftUp[1~n] 구하기
for (int now = 2; now <= n; now++)
{
int longest = 0;
for (int idx = now-1; idx >= 1; idx--)
{
if (pillar[idx] > pillar[now]) // 기둥높이가 더 높으면
{
if (LeftUp[idx] > longest) // 최대 하이라이트 구하기
longest = LeftUp[idx];
}
}
LeftUp[now] = 1+longest;
}
// RightUp[1~n] 구하기
for (int now = n-1; now >= 1; now--)
{
int longest = 0;
for (int idx = now+1; idx <= n; idx++)
{
if (pillar[idx] > pillar[now])
{
if (RightUp[idx] > longest)
longest = RightUp[idx];
}
}
RightUp[now] = 1 + longest;
}
int result = -1;
for (int idx = 1; idx <= n; idx++)
{
int l = LeftUp[idx] + RightUp[idx];
if (result < l)
result = l;
}
cout << result - 1;
return 0;
}
SWEA 햄버거 다이어트 ( 0-1 냅색 )
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com

#include <bits/stdc++.h>
using namespace std;
int Flavor[21];
int Calorie[21];
int dp[21][10001]; // dp[i][j] : i번까지 고려했고 최대칼로리 j일 때의 맛의 최대합
// j>= Calorie[i] 일 때,
// (i번째 넣는 것과 안넣는 것 비교하기)
// dp[i][j] = dp[i-1][j-Calorie[i]] + v[i] vs dp[i-1][j]
// j < Calorie[i] 일 때,
// (이전 상태 유지)
// dp[i][j] = dp[i-1][j];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
//freopen("input.txt", "r", stdin);
int T; cin >> T;
for (int t = 1; t <= T; t++)
{
memset(dp, 0, sizeof(dp));
int N, L;
cin >> N >> L; // 재료개수, 최대칼로리
for (int n = 1; n <= N; n++)
cin >> Flavor[n] >> Calorie[n];
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= L; j++)
{
if (j >= Calorie[i])
dp[i][j] = max(dp[i - 1][j - Calorie[i]] + Flavor[i], dp[i - 1][j]);
else
dp[i][j] = dp[i - 1][j];
}
}
cout << "#" << t << " " << dp[N][L] << '\n';
}
return 0;
}